はじめに
1637年、フランスの数学者ピエール・ド・フェルマーは、ギリシャの数学者ディオファントスの著書『算術』の余白に、後世に大きな影響を与える一つのメモを残した。
「xのn乗+yのn乗=zのn乗という方程式を満たす正の整数x、y、zは、nが3以上の場合には存在しない」という主張と共に、「私はこれを証明する素晴らしい方法を見つけた。
しかし、この余白は狭すぎてここには書ききれない」という言葉を添えたのである。
この一見シンプルな命題は、その後350年以上もの間、世界中の数学者たちを魅了し、苦しめ続けることとなった。
問題の本質
フェルマーの最終定理は、一見すると中学生でも理解できるほど単純な数式で表現できる。
ピタゴラスの定理(a²+b²=c²)は、直角三角形の辺の長さの関係を表す基本的な定理として広く知られている。実際、3²+4²=5²(9+16=25)のように、この等式を満たす自然数の組み合わせは無数に存在する。
しかし、指数を2から3以上に変更すると、状況は一変する。
例えば、x³+y³=z³という方程式を満たす正の整数の組み合わせは存在しないのである。
これがフェルマーの主張であり、より一般的に、nが3以上の任意の自然数について、xⁿ+yⁿ=zⁿを満たす正の整数の組は存在しないと述べたのである。
証明への長い道のり
フェルマーの死後、この定理の証明を目指して多くの数学者が研究に取り組んだ。
18世紀には、スイスの数学者オイラーがn=3の場合について証明を試みたが、完全な証明には至らなかった。
19世紀には、ドイツの女性数学者ゾフィー・ジェルマンが重要な進展をもたらし、特定の条件下での部分的な証明に成功した。
1847年には、フランスの数学者ガブリエル・ラメが証明を発表したと主張したが、この試みは失敗に終わった。
しかし、この過程で代数的整数論という新しい数学分野が発展するきっかけとなった。その後も、多くの数学者たちが様々なアプローチで証明を試みたが、完全な証明には至らなかった。
現代数学による breakthrough
20世紀に入ると、数学は大きく発展し、新しい理論や手法が次々と生まれた。
1955年には、谷山豊と島田恵一という日本人数学者が、後に「谷山・志村予想」として知られることになる革新的な理論を提唱した。この予想は、一見すると全く異なる二つの数学的概念である楕円曲線と保型形式との間に深い関連があることを示唆するものであった。
1984年、ドイツの数学者ゲルハルト・フライが、フェルマーの最終定理と谷山・志村予想との間に重要な関連があることを発見した。もし谷山・志村予想が証明されれば、フェルマーの最終定理も証明できる可能性が開けたのである。
アンドリュー・ワイルズによる証明
1993年6月23日、イギリスのケンブリッジ大学で開催された数論に関する会議で、アンドリュー・ワイルズが衝撃的な発表を行った。7年間の孤独な研究の末に、フェルマーの最終定理の証明を完成させたというのである。しかし、この証明には小さな誤りが発見され、さらに1年以上の修正作業を要することとなった。
最終的に1995年、ワイルズは共同研究者のリチャード・テイラーの助けを借りて完全な証明を完成させた。この証明は200ページ以上に及び、20世紀の最先端の数学理論を駆使したものであった。
中学生でも理解できる問題の証明に、なぜこれほどの複雑さが必要だったのか。それは、この問題が数学の本質的な深さを秘めていたからに他ならない。
フェルマーの遺産
フェルマーの最終定理の証明は、単なる一つの数学的命題の解決以上の意味を持っている。この定理の証明を目指す過程で、数学者たちは新しい理論や手法を開発し、数学全体の発展に大きく貢献した。代数的整数論、楕円曲線論、保型形式論など、現代数学の重要な分野の多くが、この問題に取り組む中で発展したのである。
また、この定理は「余白に書ききれない」という謎めいた言葉とともに残されたことで、より一層人々の興味を引きつけた。フェルマーは本当に証明を知っていたのだろうか。現代の複雑な証明とは異なる、シンプルな証明法を発見していたのだろうか。これらの疑問は、今も数学者たちの心を捉えて離さない。
おわりに
フェルマーの最終定理は、数学の美しさと深遠さを示す象徴的な例となった。
一見単純な命題が、実は現代数学の最先端の理論を必要とする深い問題であったという事実は、数学の持つ神秘的な魅力を物語っている。
350年という長い時を経て完成された証明は、人類の知的探求の偉大な成果の一つとして、永く記憶されることだろう。
そして今もなお、数学者たちはより簡潔な証明方法を探し続けている。フェルマーが本当に知っていたという「素晴らしい証明」の謎は、21世紀の数学者たちをも魅了し続けているのである。
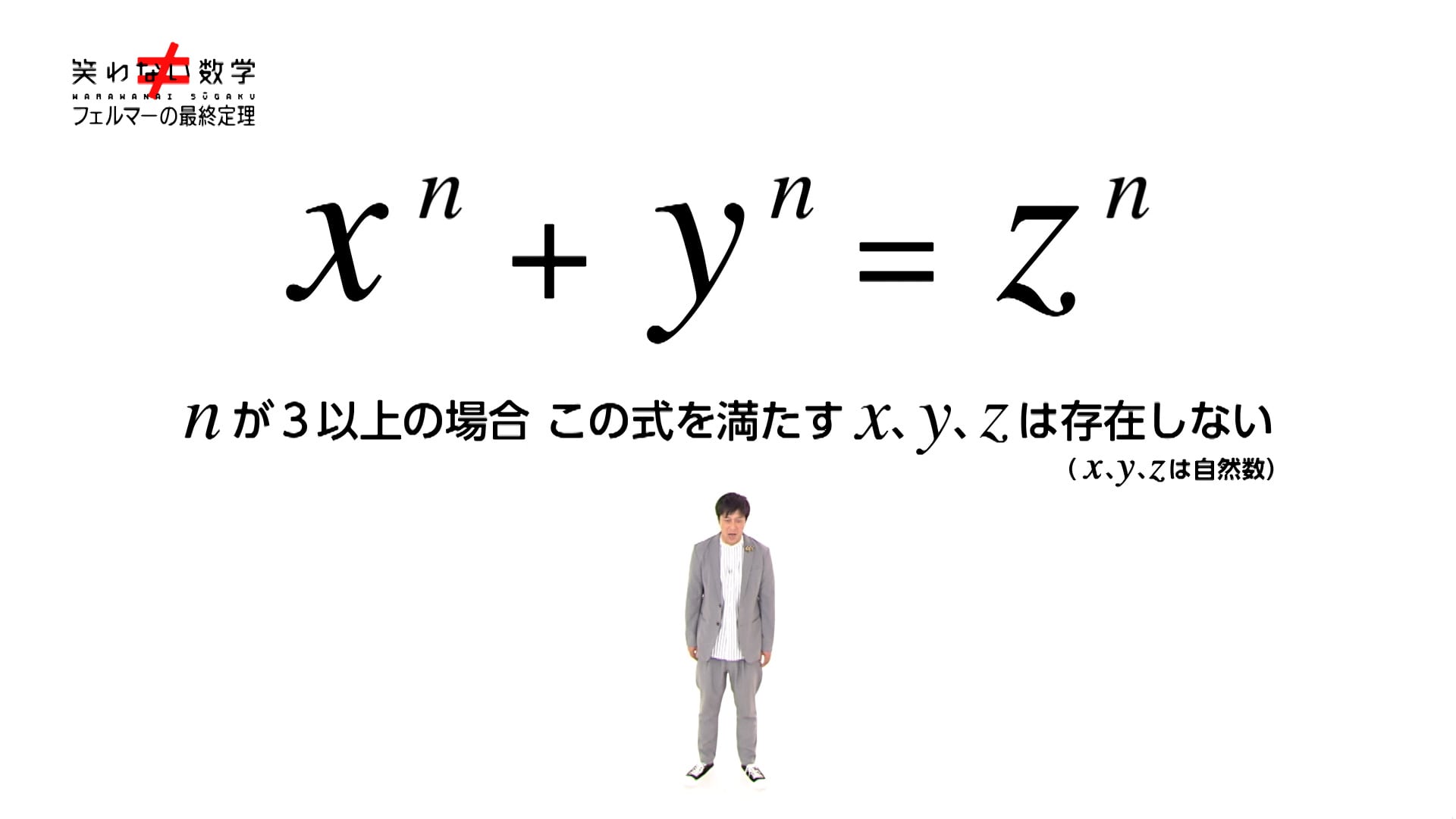
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1087c65e.d261fbdb.1087c65f.3da0bb53/?me_id=1213310&item_id=11834540&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F9712%2F9784102159712_1_3.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1087c65e.d261fbdb.1087c65f.3da0bb53/?me_id=1213310&item_id=12989648&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5261%2F9784797345261.jpg%3F_ex%3D240x240&s=240x240&t=picttext)
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/1087c65e.d261fbdb.1087c65f.3da0bb53/?me_id=1213310&item_id=21095245&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F4301%2F9784046064301_1_5.jpg%3F_ex%3D240x240&s=240x240&t=picttext)
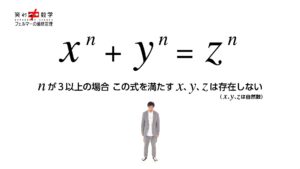










コメント